CONCEPTO LIMITES

Si la función  tiene límite  en  podemos decir de manera informal que la función  tiende hacia el límite  cerca de  si se puede hacer que  esté tan cerca como queramos de  haciendo que  esté suficientemente cerca de  siendo  distinto de .

Los conceptos cerca y suficientemente cerca son matemáticamente poco precisos. Por esta razón, se da una definición formal de límite que precisa estos conceptos. Entonces se dice:

El límite de una función f(x), cuando x tiende a c es L si y sólo si para todo , existe un  tal que para todo número real x en el dominio de la función, si  entonces .

Esto, escrito en notación formal:

Tomando valores arbitrarios de ε, podemos elegir un δ para cada uno de estos, de modo que f(x) y L se acerquen a medida que x se acerca a c.

Esta es una formulación estricta del concepto de límite de una función real en un punto de acumulación ( o punto límite) del dominio de la función y se debe al matemático francés Luis Cauchy.​

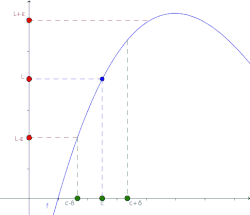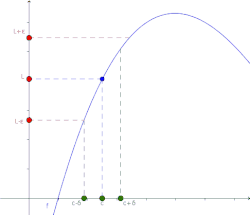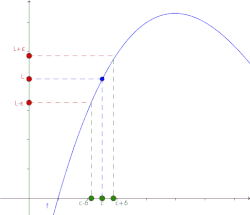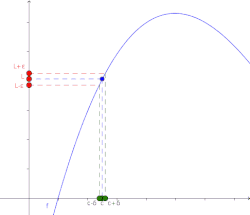
Lo importante es comprender que el formalismo no lo hacen los símbolos matemáticos, sino la precisión con la que queda definido el concepto de límite. Esta notación es tremendamente poderosa, pues nos dice que si el límite existe, entonces se puede estar tan cerca de él como se desee. Si no se logra estar lo suficientemente cerca, entonces la elección del  no era adecuada.

Veamos un ejemplo. Supongamos que se quiere demostrar que  El cálculo de este límite surge por simple sustitución, esto se debe a que la función afín es continua.