CALCULO INTEGRAL

DEFINICIÓN DE CALCULO INTEGRAL

El calculo integral, es una rama de las matemáticas que se encarga del estudio de las integrales y las anti derivadas se emplea mas para calculas aéreas y volúmenes.Fue usado principalmente por, Aristóteles, Descartes, newton y Barrow. Barrow con las aportaciones de newton creo el teorema de cálculo integral que dice: que la integración y la derivación son procesos inversos.

TEÓREMA FUNDAMENTAL DEL CALCULO INTEGRAL
El teorema fundamental del cálculo integral consiste (intuitivamente) en la afirmación de que la derivación e integración de una función son operaciones inversas. Una consecuencia directa de este teorema es la regla de Barrow, denominada en ocasiones segundo teorema fundamental del cálculo, y que permite calcular la integral de una función utilizando la antiderivada de la función al ser integrada.

METODOS DE INTERACIÓNSe entiende por métodos de integración cualquiera de las diferentes técnicas elementales usadas para calcular una antiderivada o integral indefinida de una función.Existen tambien diferentes tipos de métodos de integración, los cuales, son:-Integración directa.-Método de integración por sustitución.-Método de integración por partes.

¿QUIÉN FUE EL CREADOR DEL CÁLCULO INTEGRAL? 
Isaac Newton comparte con Leibniz el crédito por el desarrollo del cálculo integral y diferencial.Leibniz fue el primero en publicar un trabajo sobre cálculo, pero quien primero lo desarrollo fue Newton durante los años 1664 a 1666.Newton abordó el desarrollo del cálculo a partir de: La geometría analítica.Creo el Método de Fluxiones el cual son unas reglas para calcular máximos, mínimos y las tangentes (el cual no fue publicado),desarrollando un enfoque geométrico y analítico de derivadas matemáticas las cuales fueron aplicadas en curvas definidas a través de ecuaciones.

CALCULO ULTRARRÁPIDOLa capacidad para efectuar rápidamente operaciones aritméticas mentales tiene relación con la inteligencia general, intuición y creatividad matemática.Alguno de los matemáticos más sobresalientes han tenido dificultades al operar.Ejemplo:

· Carl Friedrich Gauss podía llevar a cabo impresionantes hazañas matemáticas mentales incluso antes de aprender a hablar. Una ocasión su padre estaba realizando operaciones y el resultado que el menciono resulto incorrecto, Gauss con tan solo 3 años de edad pudo resolver la operación sin ningún problema.

INTRODUCCIÓN A LA VIDA DE ARQUIMIDES DE SIRACUSAArquímedes de Siracusa, matemático, físico, ingeniero, inventor y astrónomo griego, fue un científico de la antigüedad clásica Arquímedes de Siracusa, matemático, físico, ingeniero, inventor y astrónomo griego, fue un científico de la antigüedad clásica, realizo el método del agotamiento para áreas por medio del arco de parábolas calculando por la sumatoria de la serie infinita.Se aproximo al numero π, definió el espiral y realizo formulas para volúmenes.Murió entre (214-212 a.C.) en Siracusa. Cicerón fue como su discípulo y encontró en su tumba (esfera inscrita dentro de un cilindro) que por deducción fueron 2/3 de volumen y superficie del cilindro, contando la base., realizo el método del agotamiento para áreas por medio del arco de parábolas calculando por la sumatoria de la serie infinita.Se aproximo al numero π, definió el espiral y realizo formulas para volúmenes.Murió entre (214-212 a.C.) en Siracusa. Cicerón fue como su discípulo y encontró en su tumba (esfera inscrita dentro de un cilindro) que por deducción fueron 2/3 de volumen y superficie del cilindro, contando la base.

Teoría

${\displaystyle \scriptstyle \ \int _{a}^{b}f(x)\,\mathrm {d} x}$ se interpreta como el área bajo la curva de f, entre a y b.

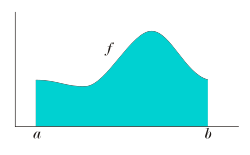
Dada una función ${\displaystyle f(x)}$ de una variable real ${\displaystyle x}$ y un intervalo ${\displaystyle [a,b]}$ de la recta real, la integral es igual al área de la región del plano ${\displaystyle xy}$limitada entre la gráfica de ${\displaystyle f}$, el eje ${\displaystyle x}$, y las líneas verticales ${\displaystyle x=a}$ y ${\displaystyle x=b}$, donde son negativas las áreas por debajo del eje ${\displaystyle x}$.

${\displaystyle \int _{a}^{b}f(x)\,{\text{d}}x}$

La palabra "integral" también puede hacer referencia a la noción de primitiva: una función F, cuya derivada es la función dada ${\displaystyle f}$. En este caso se denomina integral indefinida, mientras que las integrales tratadas en este artículo son las integrales definidas. Algunos autores mantienen una distinción entre integrales primitivas e indefinidas.

Los principios de la integración fueron formulados por Newton y Leibniz a finales del siglo XVII. A través del teorema fundamental del cálculo, que desarrollaron los dos de forma independiente, la integración se conecta con la derivación, y la integral definida de una función se puede calcular fácilmente una vez se conoce una antiderivada. Las integrales y las derivadas pasaron a ser herramientas básicas del cálculo, con numerosas aplicaciones en ciencia e ingeniería.

Bernhard Riemann dio una definición rigurosa de la integral. Se basa en un límite que aproxima el área de una región curvilínea a base de partirla en pequeños trozos verticales. A comienzos del siglo XIX, empezaron a aparecer nociones más sofisticadas de la integral, donde se han generalizado los tipos de las funciones y los dominios sobre los cuales se hace la integración. La integral curvilínea se define para funciones vectoriales de una variable, y el intervalo de integración [a,b] se sustituye por el de la parametrización de la curva sobre la cual se está integrando, la cual, conecta dos puntos del plano o del espacio. En una integral de superficie, la curva se sustituye por un trozo de una superficie en el espacio tridimensional.

Las integrales de las formas diferenciales desempeñan un papel fundamental en la geometría diferencial moderna. Estas generalizaciones de la integral surgieron primero a partir de las necesidades de la física, y tienen un papel importante en la formulación de muchas leyes físicas cómo, por ejemplo, las del electromagnetismo. Los conceptos modernos de integración se basan en la teoría matemática abstracta conocida como integral de Lebesgue, que fue desarrollada por Henri Lebesgue